Non-interference in dimension 6 EFT: beyond LO & 2 to 2 processes
People interested (add your name): Francesco Riva, Ken Mimasu, Benjamin Fuks, Julia Harz, Kristin Lohwasser, Fabio Maltoni, Jorge de Blas, Daniele Barducci, Minho Son, Haiying Cai, Olivier Mattelaer, Adam Falkowski, Davide Lombardo
Investigate the impact of higher order corrections or additional radiation on high energy 2→2 processes involving dimension 6 EFT operators that have been shown not to interfere at leading order.
A simple test case may be $W^+ W^-$ production at a lepton collider. Here the EW corrections including dimension 6 operators have not been calculated but an extra photon (or any extra vector) emission would alter the helicity structure and is part of the higher order contribution.
We focus on the operator that generates transverse helicity, schematically O_{3W}= W_{\mu\nu}^3
References:
- “Helicity selection rules and noninterference for BSM amplitudes” (arXiv)
- “Testing gluon selfinteractions in three jet events at hadron colliders” (arXiv)
Helicity amplitude from madgraph (2 to 2 and 2 to 3):
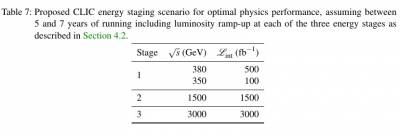
Benchmark parameters from CLIC [https://arxiv.org/abs/1608.07537 – Updated baseline for a staged Compact Linear Collider]
accelerator design foresees 80% electron polarisation.
stages running with different CME and luminosity:
To Do: 1) Read References (in particular Dixon&Shadmi) 2) Compute Amplitude for e^+ e^- → W^+ W^- and e^+ e^- → W^+ W^- \gamma or Z in the SM first and with the above dimension-6 operator 3) Expand in m_W/Energy and in g^'→0 to have simpler expressions 4) Check with MG5 the analog of the angular distributions of Dixon/Shadmi 5) Asses, as function of the collision energy, luminosity and systematic errors, wheter the best reach on c_{3W} is given by processes with 3 final states or two
Further Questions Also loop effects generate interference. Yet this is small compared with the tree-level SM^2 contribution to the same amplitude. Instead for real emission both the leading SM^2 and interference are suppressed. Do Sudakov effects play a role here? can they enhance virtual loops?