Les Houches
2023 Session
-
- Use of wiki pages and slack. Wifi access/set-up.
- Important info about bus, lodging, facilities.
- Bulletins.
Wikis of Previous sessions
Les Houches Themes
(Lyrics and Music)
(Lyrics and Music)
Susan Shotkin Gascon-Shotkin, Linda Finco, Sijing Zhang, Grégory Moreau, Peter Richardson, Sylvain Fichet, David Grellscheid, Jon Butterworth, David Yallup…
Joint with Higgs group. Other projects using Contur.
Herwig not dealing with UFO file properly. PR aiming to fix the 3D vertex.
This is now fixed. Peter has implemented the relevant vertices in Herwig/ThePEG and its UFO interface, and validated the cross section against MadGraph. This is not yet in 7.1.1 but is in the Herwig 7 trunk in the
repository, hopefully in next release. The exception is the 5-point vertices which are used in the CP-even model:
Warning: Lorentz structure VVVVS ( g g g g phiNP ) in V_49 is not supported. Warning: Lorentz structure VVSSS ( W- W+ H H phiNP ) in V_118 is not supported. Warning: Lorentz structure VVVVS ( a a W- W+ phiNP ) in V_122 is not supported. Warning: Lorentz structure VVVVS ( W- W- W+ W+ phiNP ) in V_126 is not supported. Warning: Lorentz structure VVVVS ( a W- W+ Z phiNP ) in V_150 is not supported. Warning: Lorentz structure VVSSS ( Z Z H H phiNP ) in V_156 is not supported. Warning: Lorentz structure VVVVS ( W- W+ Z Z phiNP ) in V_160 is not supported.
These are currently ignored - hope they aren't a major effect (they don't look like they should be…)
Suggested parameter ranges from Sylvain:
CP-even scalar: mphi in [10, 100] GeV f0B in [1, 10] TeV f0W in [1, 10] TeV f0H in [1, 10] TeV
CP-odd scalar: mphi in [10, 100] GeV f0B in [1, 10] TeV f0W in [1, 10] TeV
For each case, all the other f's should be set to very large values.
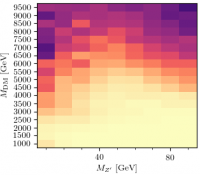
So, here is a scan using these ranges for the CP-odd scalar model (f0 value labelled $\Lambda$ on the vertical axis, $M_\phi$ on the horizontal. Hetmap and 95% exclusion contour.
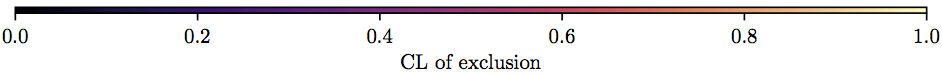
… so this looks promising. Everything excluded except the lowest mass/highest scale. This needs to be carefully checked, of course - see below. Basically all the yellow region above is excluded by the ATLAS diphoton cross sections: arXiv:1704.03839. If those are not included, the ATLAS $Z+\gamma$ measurements (in dilepton+photon and MET+photon) have quite some power on their own, see below.
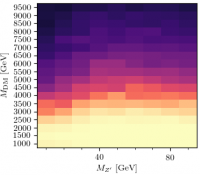 $(l^+l^-)$ or $(l + E_T^{\rm miss}) + \gamma$
$(l^+l^-)$ or $(l + E_T^{\rm miss}) + \gamma$
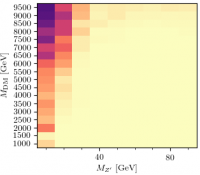
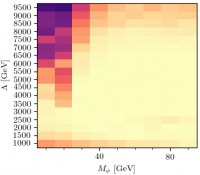 $E_T^{\rm miss} + \gamma (\gamma)$
$E_T^{\rm miss} + \gamma (\gamma)$
 Inclusive and di-photons
Inclusive and di-photons
Here are the plots from some of the points on the grid. (See here for an explanation of the plot format.)
Page of plots: The most powerful exclusion in the 8 TeV data comes from the $\gamma + E_T^{\rm miss}$ channel, specifically the $E_T^\gamma$ differential cross section for events with no jets, in this paper. There is also some exclusion from the $\tau$ distribution in the $H \rightarrow \gamma\gamma$ paper - see below for more on that. Also once the 7 TeV data are included, the inclusive and diphotons cover this point on their own.
Page of plots: Another low mass, moderate coupling point. Chosen because for this one, diphoton measurements give the most powerful exclusion for the 8 TeV data set (although $\gamma + E_T^{\rm miss}$ still contributes, and once 7 TeV are included, the photon measurement would rule this point out too). The inclusive diphotons would contribute at low $M_{\gamma\gamma}$, because the 20 GeV mass of the $\phi$ now sneaks into the measurement at the bottom of the range, but the most sensitive plot in the diphoton category (and thus the one chosen by Contur) is again from the Higgs paper, this time $p_T^{\gamma\gamma}$. This is maybe surprising because the Higgs measurement has a mass window cut at $105 < M^{\gamma\gamma} < 160$ GeV, much higher than $M_\phi$. The contribution to the Higgs fiducial phase space seems to be coming from $q\bar{q} \rightarrow \phi \gamma$ events, where the additional photon pairs with one of the $\phi$ decay products. This interesting but should probably not be taken face value because it is not clear how such a contribution would impact on the continuum in the fits used to extract the $H \rightarrow \gamma\gamma$ cross section.
Page of plots: This point is chosen to look at the higher end of the $M_\phi$ range, where the sensitivity is greater, and so we look at a high $\Lambda$ value. Again the sensitivity is driven by this paper, but now it is the $\gamma\gamma + E_T^{\rm miss}$ cross section that does the work. And again once the 7 TeV data are included, the inclusive and diphotons cover this point on their own.
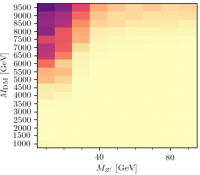
A similar run for the CP-even scalar model, using the parameters sugested by Sylvain, gives the heatmap below:
This is 7 and 8 TeV only, but the currently available 13 TeV results have no real impact as there are no photon measurements in Rivet yet. Again, the inclusive diphotons and the Z+jet results both have significant sensitivity.
 $(l^+l^-)$ or $(l + E_T^{\rm miss}) + \gamma$
$(l^+l^-)$ or $(l + E_T^{\rm miss}) + \gamma$
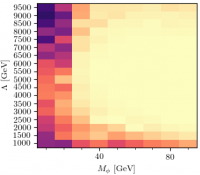 $E_T^{\rm miss} + \gamma$
$E_T^{\rm miss} + \gamma$
 Inclusive and di-photons
Inclusive and di-photons
Note that the sensitivity at low $M_\phi$ and $\Lambda$ is somewhat reduced, especially for the $E_T^{\rm miss} + \gamma$ channel. Presumably something to do with the angular distributions of the decay photons of the $\phi$, but to be studied…
There is still 95% exclusion even at the highest $\Lambda$ values studied. Would be interesting to see how far it goes. Update - not very far? Here's an 8 TeV run going to higher values.
Remember, big caveat on all this is the standard Contur assumption (at the moment) that the data exactly agree with the SM, which means (given we only really know that these data are consistent with the SM) that we are neglecting the SM theory uncertainties.